Number Classification
All number categories, from Complex to Counting
Mathematics is unique. The unique science if everyone could agree that it is Science. But, it's also hard to argue that it is not Art. Math is absolutely certain, except the cases when it is not ("as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality"). Still having no one general definition, math doesn't even bother to have one opinion on such the fundamental building block as Numbers. Nevertheless, math is an important part of almost every field of science, engineering, and human life.
Here is the most common and well-accepted number classification tree:
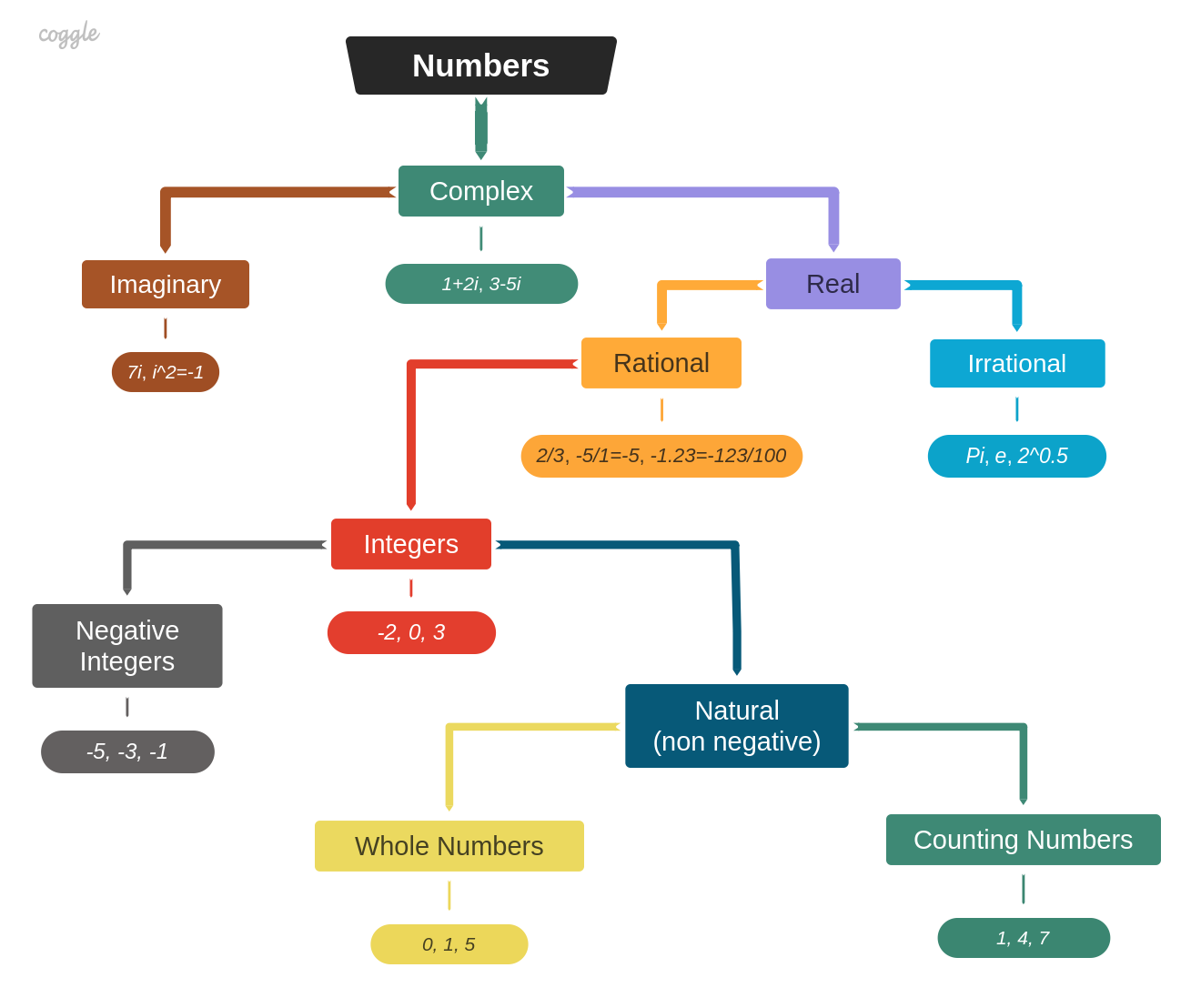
It also shouldn't be a surprise to find slight distinctions in the meaning of the same essences in Math and Computer Science (CS):
- Natural numbers. In Math, they are meant to be Positive Integers (1, 2, 3, ...), but in CS they are non-negative Integers which include Zero (0, 1, 2, 3 ...)
- Mantissa. In Math, it is a fractional part of the logarithm. In CS, it is significant digits of a floating-point number (thus, quite often are used other definitions in this case, like significand and coefficient)
There is a quite related topic in terms of the values which a variable can take on. In mathematics, a variable may be two different types: continuous and discrete:
- A variable is continuous when it can take on infinitely many, uncountable values. There is always another value in between two others in a non-empty range, no matter how close they are.
- A variable is discrete when there is always a positive minimum distance between two values in a non-empty range. The set of numbers is finite or countably infinite (e.g. Natural numbers)
The understanding of the discreteness is crucial in Computer Science as all real-world computers internally work only with discrete data (which makes it challenging to represent Irrational numbers). All existing computability theories (e.g. Turing thesis, Church thesis) are defined on discrete values, and the domain is the set of Natural numbers.