Turing: thesis, machine, completeness

on 2019-12-15 in note about cs mindmap ~1 min read

A formal system in the computability theory

Alan Turing is one of the pioneers of the computability theory and logic formalization. He came up with the hypothesis of which algorithms can be implemented and computed by machines (Turing's thesis), created an abstract model of such machine (Turing machine), and described absolutely vital abilities of any system for being able to realize any logic that can be computed (Turing completeness).

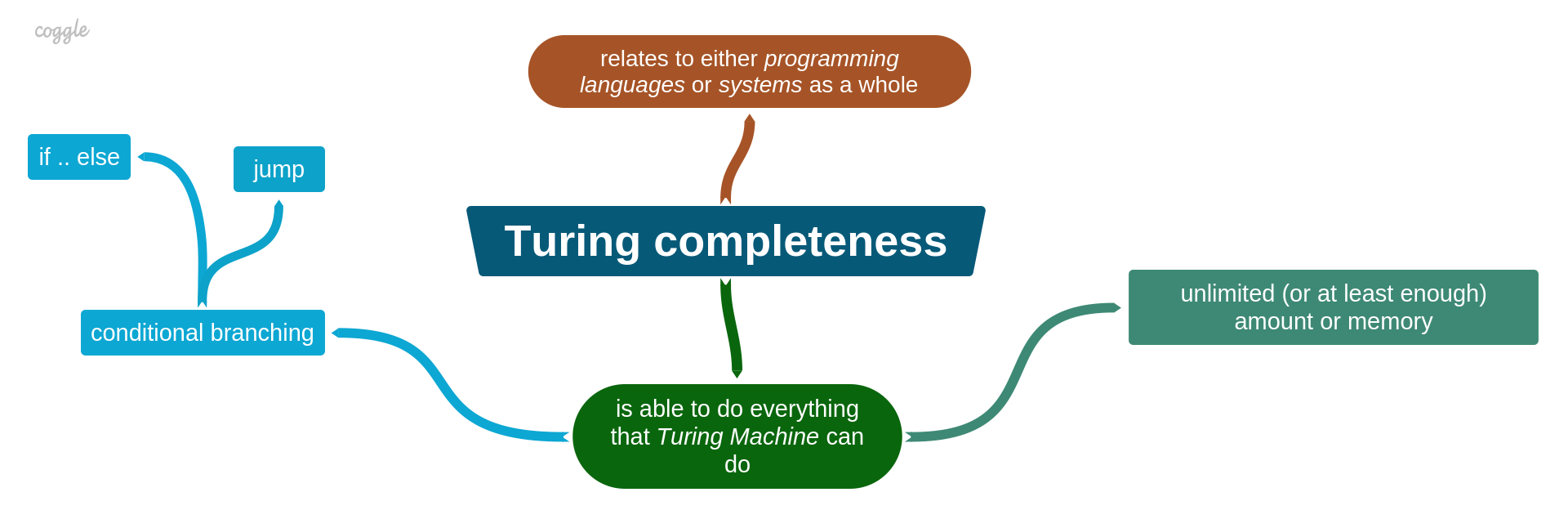
Turing's thesis is only one of the existing formal systems in the computability theory. There are also λ-calculus, Markov algorithms, but they all were implemented on the Turing Machine that is used at this time as a general computational model to classify which real-world systems (mostly programming languages) are able to compute mathematical functions or implement algorithms.

All existing computability theories are defined on discrete values, and the domain is the set of Natural numbers.

I prepared several mindmaps to summarize basic ideas and statements:

Turing's thesis:

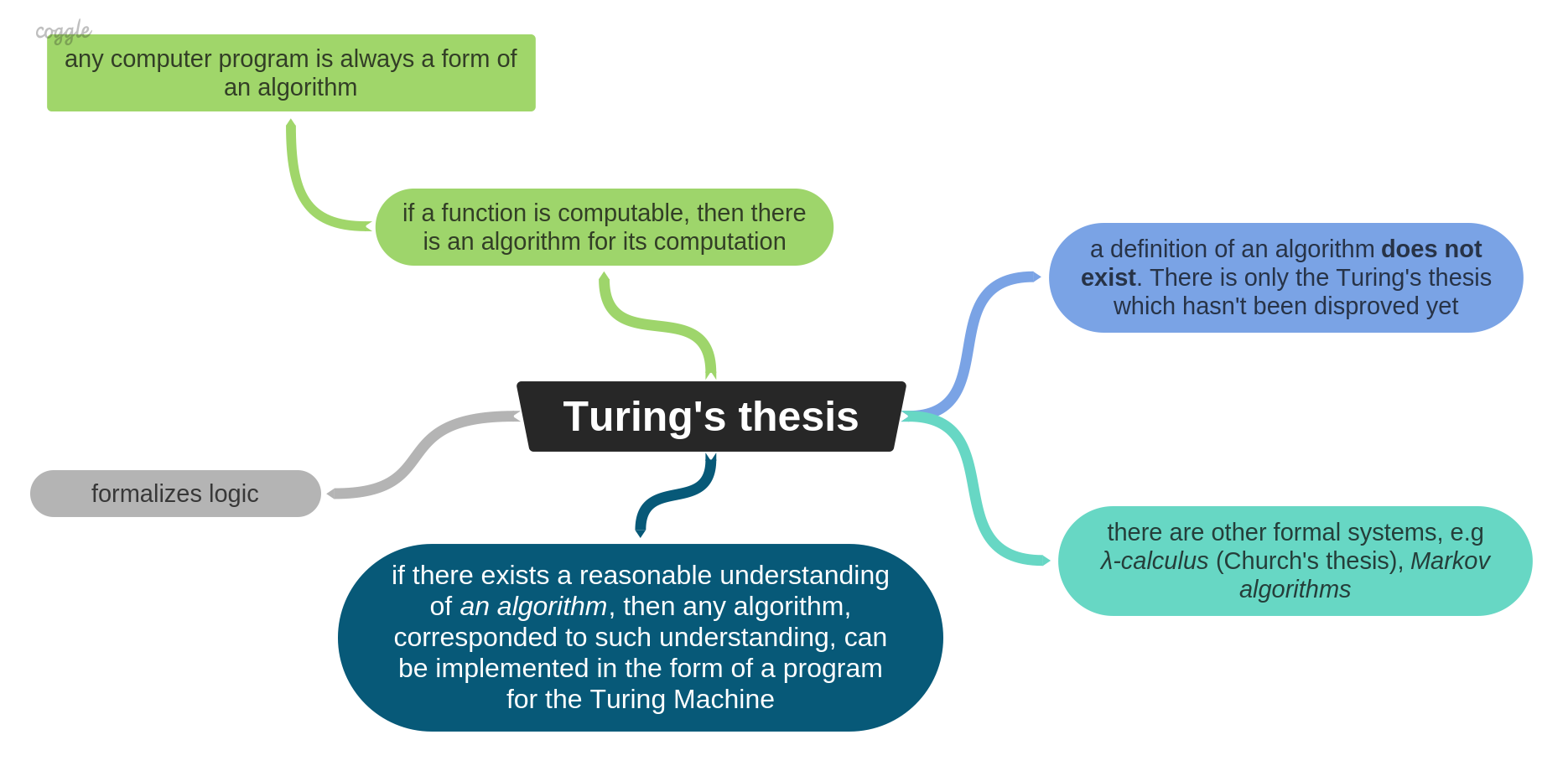
Turing machine:

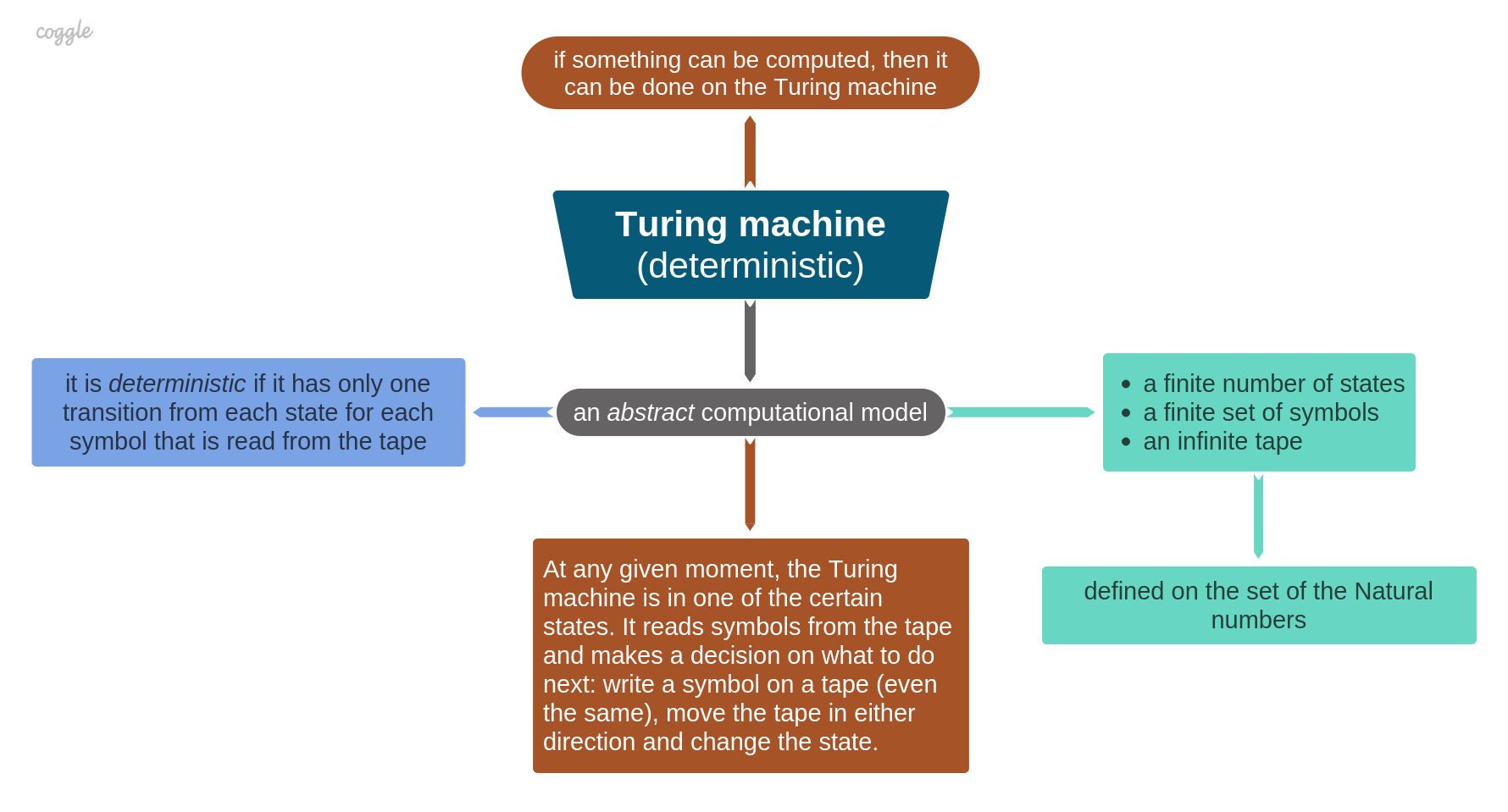
Turing completeness:

Found a bug or typo? Please, send me feedback or submit a PR on Github.

This is my personal blog. All ideas, opinions, examples, and other information that can be found here are my own and belong entirely to me. This is the result of my personal efforts and activities at my free time. It doesn't relate to any professional work I've done and doesn't have correlations with any companies I worked for, I'm currently working, or will work in the future.